On the Network Effects of Stores of Value

This post is a spiritual successor to The Smart Contract Network Effect Fallacy.

Bitcoin has a network effect. Many crypto evangelists assert that the network effect of Bitcoin is so strong that hyperbitcoinization is inevitable.

But this is not quite right. Bitcoin’s network effect as digital gold is not what many assert that it is. Network effects are nuanced, and generally misunderstood.

In this essay, I’ll explore the network effects of Bitcoin as digital gold, and as digital cash. I’ll also explore other competitive moats that are not network effects.

For general background, I recommend this Medium post, this a16z slideshow, this Techstars post, and this post on data network effects. For longer-form reading on network effects and technology platforms more generally, I recommend Platform Scale and books by the author Sangeet Choudary.

Foundations Of Network Effects

Network effects are an emergent property that occur when:

A product or service becomes more valuable to its existing users as more people use it.

There are a few different kinds of network effects:

Direct Network Effects — increases in usage lead to direct increases in value.

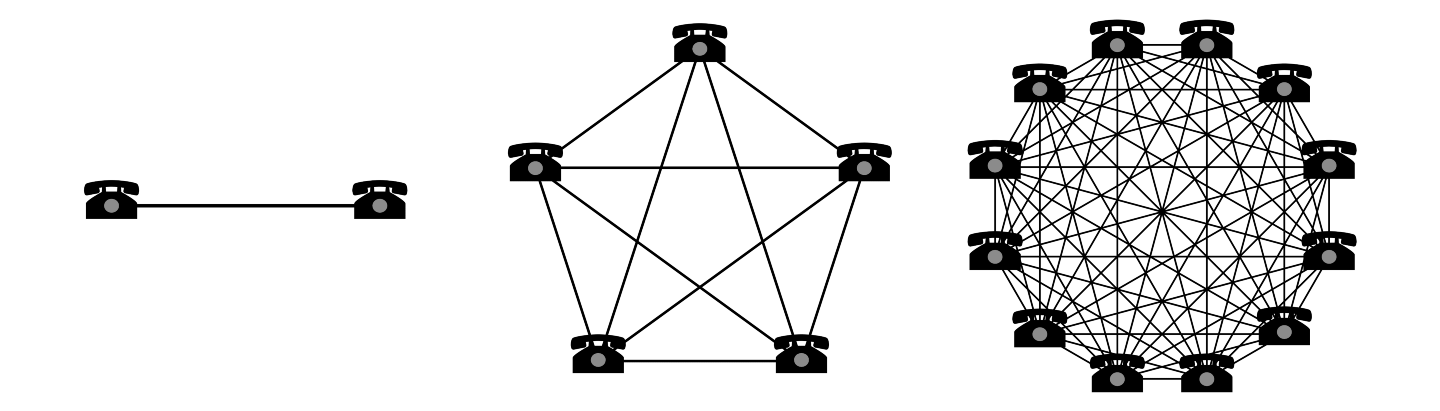
Direct network effects work because existing users gain the option to interact with an increasing number of people as the underlying product/service is adopted. Basically all closed-loop communication networks exhibit this type of network effect, including Internet-based services such as Facebook and Whatsapp.

Indirect Network Effects — increased usage of the product spawns the production of increasingly valuable complementary goods, which results in an increase in the value of the original product. Operating systems (OS) are the most famous type of product that benefit from indirect network effects. App developers are drawn to build on an OS to reach consumers; by building an app for a given OS, that OS becomes more attractive to new consumers, creating a larger market for future app developers.

Two Sided Network Effects — increases in usage by one set of users increases the value of a complementary product to another distinct set of users, and vice versa. Some famous examples include eBay, Uber and Lyft, AirBnB, and Amazon’s marketplace business. In each of these networks, consumers benefit from more choice and competition among suppliers, which drives more consumers, which attracts more suppliers.

Data Network Effects — when a product, generally powered by machine learning, becomes smarter as it acquires more data users. Data network effects occur in most modern cloud-based apps today, though their relative strengths vary widely by use case and sophistication.

Quantifying The Strength Of Network Effects

Measuring the precise strength of network effects is rather difficult. It’s not an exact science.

It’s particularly challenging because the marginal value of additional users to the system changes over time. For example, many of my friends have begun to delete their Facebook profiles in the last few years. Facebook is approximately just as useful to me now as it was 3 years ago. The loss of 5% or even 10% of my Facebook friends has relatively little impact on my Facebook experience because I still have 500 other friends who use Facebook.

It is often said that the defensive moat of a network-effect bound business can be quantified using Metcalfe’s Law, which states that the value of a network is proportional to the square of the number of users. For readability, it can be said the network effect of businesses that are subject to Metcalfe’s law have a network effect of n2.

Since Metcalfe proposed this working definition of the value of a network, it’s been thoroughly debunked. There are no known networks that exhibit a network effect of n2 in perpetuity as they grow. Moreover, the original assumption driving n2 was that all connections in a network are equally valuable. Instead, it’s it’s more commonly recognized that the network effects of most networks are likely closer to n*log(n) than n2.

While this certainly makes more sense than n2 (nothing can grow quadratically forever), even n*log(n) is a perpetually super-linear curve. What we see in reality is that not only are all connections not equally valuable, but that after a certain point, the value of each marginal connection in the system begins to decrease (e.g. the next 10M Facebook users in Asia are worth very little to existing American users).

In practice, best case network effects resemble an S-curve more than n2 or n*log(n).

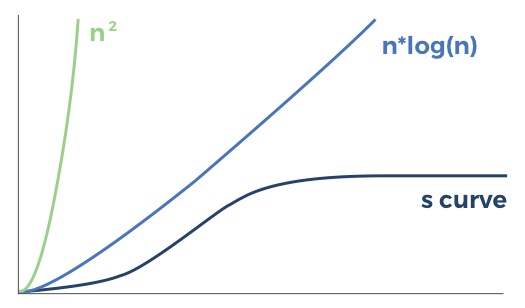
There are many case studies that empirically demonstrate the S-curve nature of network effects in practice. This is why the Macintosh survived the 90s (if the network effect of Windows was actually n2, Apple probably wouldn’t have survived), why there are so many messaging apps (Whatsapp, Telegram, Facebook Messenger, Signal, etc), why Lyft can effectively compete with Uber (I don’t care how many drivers are on the road as long as I get a car in less than two minutes), and why so many specialty e-commerce stores can compete with Amazon.

Why do people continue to say that networks are subject to n2 or n*log(n) network effects given the very high-profile examples as evidence to the contrary? Because in all three curves, it’s very hard to discern the difference between the left-most part of each curve:

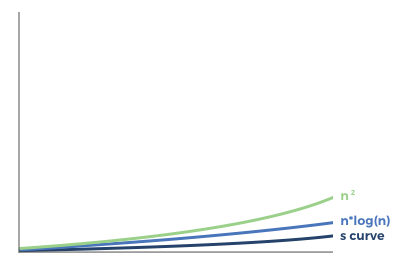
It’s the right half of each curve — the part that only occurs once a network has achieved critical mass — in which these three curves materially diverge. The n2 curve continues to accelerate upwards quadratically. The n*log(n) curve also accelerates upwards in perpetuity, albeit at a much lower rate. On the other hand, the S-curve turns from super-linear to sub-linear as the network crosses some saturation point.

Of course, not all networks are subject to identical S-curves. And not all networks are even subject to the best-case network effects of an S-curve.

Some network effects never achieve exponential-like network effects such as the left half of the S-curve. Some networks are only subject to log(n) network effects from inception, making them perpetually sub-linear, as opposed to the S-curve, which is super-linear at first.

The most common example of a log(n) network effect is an exchange for a liquid, fungible good. Even if you make the very aggressive assumption that each additional user increases daily liquidity, the marginal value of that extra liquidity becomes increasingly worthless to all existing users. This holds true even from the earliest days of a network. This curve is never super-linear; it’s always sub-linear.

Let’s consider a simple case in which each new user trading for some fungible good adds .01% to the daily liquidity of the good.

When there are 100 users, daily liquidity is 1% of the market cap of the good.

When there are 1,000 users, daily liquidity is 10% of the market cap of the good.

When there are 10,000 users, daily liquidity is 100% of the market cap of the good.

When there are 100,000 users, daily liquidity is 1,000% of the market cap of the good (10x daily turnover).

If a user owns .1% of the goods in being traded, the value of the liquidity provided by each marginal users becomes increasingly worthless. Technically, slippage will decrease as the number of users and therefore liquidity grows, but in practice the marginal liquidity benefit will be so low that it will be imperceptible not just to a given user, but all existing users.

All exchanges for a given fungible asset have a network effect of approximately log(n), which can be visualized as follows:

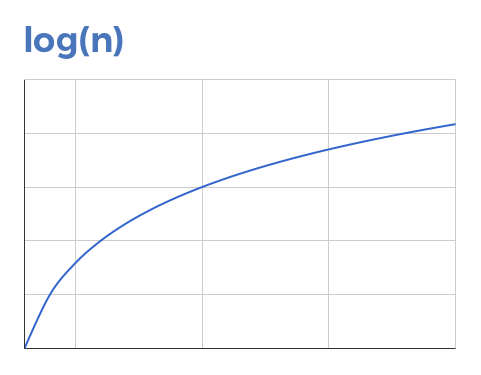
There is ample evidence that this is empirically true. If the network effects of exchanges for fungible goods were super-linear at any point on the curve, we wouldn’t have so many crypto exchanges. What we can observe is that if an exchange has some liquidity — a fraction of that of the market leader — it’s often enough to sustain a viable exchange, and to provide reasonable liquidity to market participants.

The Network Effect Of Digital Gold

Which type of network effect does digital gold exhibit?

To answer this question, let’s walk through the mechanics of how users will use digital gold.

The purpose of a store of value such as digital gold is to… store value for consumption at some later date. Other than the time in which the digital gold is converted into something else, digital gold just sits there, doing nothing. It doesn’t benefit from the addition or removal of new users.

When a user wants to liquidate their digital gold to consume some other good or service, she needs to find liquidity: someone who is willing to purchase the digital gold. This can be done at an exchange that specializes in fungible digital gold.

The utility of digital gold is a function of its liquidity. As described above, this means that the network effect for Bitcoin can be approximated as log(n).

The Network Effect Of Digital Cash

Which type of network effect does digital cash exhibit?

To answer this question, let’s walk through the mechanics of how users will use digital cash.

The purpose of digital cash is to both store value and be used as a medium of exchange. Additionally, digital cash can become a unit of account.

The utility of digital cash in aggregate therefore is a function of how many merchants want to accept payment for goods and services in digital cash.

This resembles the direct network effect (the telephone diagram) as described above. The more people who accept payment using digital cash, the more merchants existing users can do business with.

All major global currencies exhibit this network effect in their respective jurisdictions. Because merchants and consumers must pay taxes in each jurisdiction in the native fiat currency of their country, they choose to receive wages (employees) and revenues (businesses) in the form of the local fiat currency. This creates a powerful network effect, as very few people want to take on the balance sheet risk of holding a currency that’s subject to price-fluctuations relative to the currency with which they purchase goods/services and pay taxes with.

Intuitively, this is likely to be subject to an S-curve network effect. The first 50% merchants that accept digital cash for payment make it exponentially more useful than the second 50%.

Store Of Value Vs Utility

Bitcoin maximalists will argue that the argument presented above is based on semantics. Specifically, they’ll argue “Of course new users will make Bitcoin more valuable. They’ll buy it and hold it, by definition making it more valuable! The liquidity argument is a red herring.”

While this is true in a narrow sense, it ignores the competitive reality: what if something else becomes digital cash and achieves a super-linear network effect? That’s the broader point I’m making. The sub-linear network effect of liquidity alone is, in isolation, a red herring. But if something else becomes digital cash with a super-linear network effect while Bitcoin remains digital gold with a sub-linear network effect, then Bitcoin will be surpassed.

In crypto circles, this framing is often presented as the store of value (SoV) vs. utility debate. The SoV view is based upon reflexivity: The more people hold it, the more valuable it becomes, therefore driving more people to hold it.

Of course, reflexivity works going up and down. This creates excessive volatility and therefore instability, defeating the purpose of a store of value entirely. It’s very easy to believe the SoV hypothesis when the price only increases. But when the price decreases, the underlying value of the utility value creates an organic price floor.

It’s easy forget how early we are with regard to cryptocurrency. There are 7 billion people on Earth. Less than 50 million have any cryptocurrency. We’re at less than 1% global saturation. In a world of open-source software where every feature can be copied, the key to winning is to achieve network effects as quickly as possible. And this is why the strength of the underlying network effect is so important. Over tens and hundreds of millions of users, these benefits compound (or fail to), creating massive differences in the terminal value of the network.

Other Moats

Network effects are just one type of competitive moat. There are many types of moats.

The other moats that Bitcoin maximalists espouse are “brand recognition” and third-party ecosystem integrations such as exchanges, ATMs, other financial products, hardware and mobile wallets, etc.

To explore the power of these moats, I’ll compare Bitcoin against Ethereum. This is not to suggest that Ethereum specifically is likely to overtake Bitcoin. Rather, it’s mean to serve as an example of what a competitive network can achieve in less than three years since launch.

Brand recognition is indeed a moat. Bitcoin is the leader among cryptocurrencies. But to suggest that its brand is somehow untouchable is simply false. No brand is untouchable.

There is not a good way to measure brand value of an open, permissionless brand like Bitcoin, but we can use Google trends as a crude measurement tool.

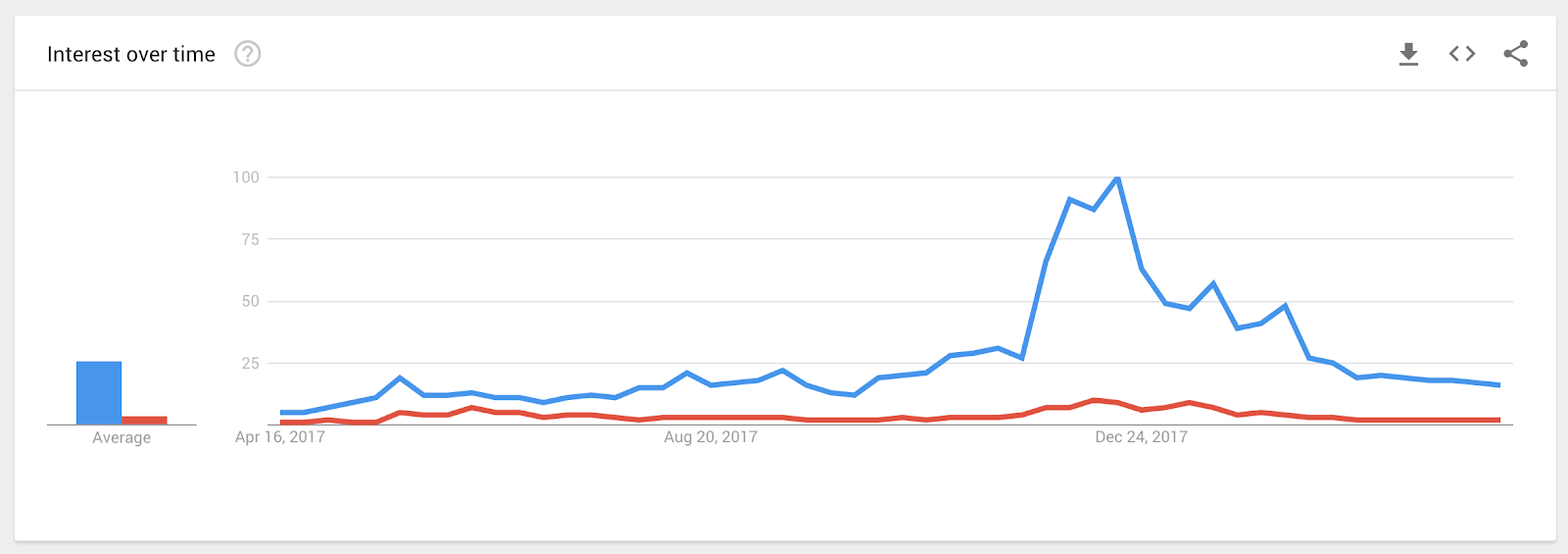
Bitcoin is blue, Ethereum is red. At the time of largest divergence, Bitcoin was about 11x as frequently searched as Ethereum. Today, the difference is 8x. Given how volatile and rapidly evolving the space is, this lead could be wiped out within a few years.

What about third-party integrations? Here, Ethereum is almost on par with Bitcoin:

Exchanges — All major exchanges support fiat pairs with Bitcoin and Ethereum.

Hardware wallets — All major hardware wallets support both Bitcoin and Ethereum.

ATMs — To the best of my knowledge, all crypto ATMs support both.

Mobile wallets — Both Bitcoin and Ethereum have a plethora of mobile wallets for iOS and Android.

Other financial products — Bitcoin has a lead with CME, CBOE, and NASDAQ futures. But given Ethereum’s trajectory, it seems quite reasonable that it will achieve parity within 24 months.

Again, my point is not that Ethereum is set to overtake Bitcoin, but rather that the range of 3rd party integrations is not insurmountable.

Conclusion

Network effects and competitive moats are generally misunderstood. Contrary to popular belief, there are no networks that exhibit n2 network effects, and in fact many exhibit log(n) network effects, notably fungible asset exchanges. Bitcoin as digital gold will be subject to the perpetually sub-linear log(n) network effect, whereas Bitcoin as digital cash can achieve super-linear network effects as crypto adoption grows from <1% to 50% of the global population. The cryptocurrency that becomes the dominant store-of-value will by definition need to exhibit super-linear network effects as it grows.

Moreover, other types of competitive moats such as brand and broader ecosystem integrations do not exhibit increasing returns to scale, and can be easily overcome by a competitive network with super-linear network effects. We already have ample evidence that this is true.

The battle to be the super-mega winner of crypto is just beginning. On the left-most 1% of all of the network effect curves, the differences are not easily discernible. It’s easy to think that network effects have started to kick in before they actually have.

Thanks to Chris Dixon and Matt Huang for providing feedback on this essay.